凤凰院魔法使のBlog

算法题解[模拟]P1065作业调度方案题解[NOIP2006提高组]

发表于 分类于
本文字数： 4.8k 阅读时长 ≈ 4 分钟
经典模拟算法——P1065[NOIP2006提高组]作业调度方案题解

题目描述

我们现在要利用 $m$ 台机器加工 $n$ 个工件，每个工件都有 $m$ 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。

每个工件的每个工序称为一个操作，我们用记号 j-k 表示一个操作，其中 $j$ 为 $1$ 到 $n$ 中的某个数字，为工件号；$k$ 为 $1$ 到 $m$ 中的某个数字，为工序号，例如 2-4 表示第 $2$ 个工件第 $4$ 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。

例如，当 $n=3,m=2$ 时，1-1,1-2,2-1,3-1,3-2,2-2 就是一个给定的安排顺序，即先安排第 $1$ 个工件的第 $1$ 个工序，再安排第 $1$ 个工件的第 $2$ 个工序，然后再安排第 $2$ 个工件的第 $1$ 个工序，等等。

一方面，每个操作的安排都要满足以下的两个约束条件。

  1. 对同一个工件，每道工序必须在它前面的工序完成后才能开始；

  2. 同一时刻每一台机器至多只能加工一个工件。

另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。

由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为 1 1 2 3 3 2。

还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。

例如，取 $n=3,m=2$，已知数据如下（机器号/加工时间）：

工件号　工序$1$　　工序$2$
$1$$1/3$$2/2$
$2$$1/2$$2/5$
$3$$2/2$$1/4$

则对于安排顺序 1 1 2 3 3 2，下图中的两个实施方案都是正确的。但所需要的总时间分别是 $10$ 与 $12$。

　

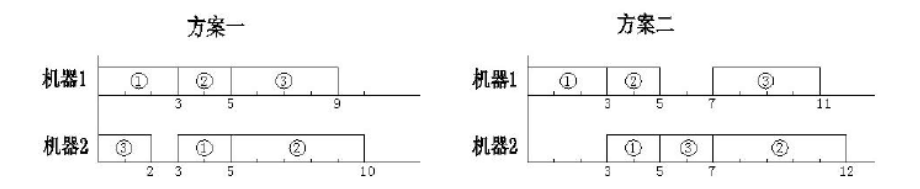
当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件（$1$）（$2$）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（$1$）（$2$）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。

显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

输入格式

第 $1$ 行为两个正整数 $m$, $n$，用一个空格隔开，
（其中 $m(<20)$ 表示机器数，$n(<20)$ 表示工件数）

第 $2$ 行：$m \times n$ 个用空格隔开的数，为给定的安排顺序。

接下来的 $2n$ 行，每行都是用空格隔开的 $m$ 个正整数，每个数不超过 $20$。

其中前 $n$ 行依次表示每个工件的每个工序所使用的机器号，第 $1$ 个数为第 $1$ 个工序的机器号，第 $2$ 个数为第 $2$ 个工序机器号，等等。

后 $n$ 行依次表示每个工件的每个工序的加工时间。

可以保证，以上各数据都是正确的，不必检验。

输出格式

$1$ 个正整数，为最少的加工时间。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
2 3
1 1 2 3 3 2
1 2 
1 2 
2 1
3 2 
2 5 
2 4

样例输出 #1

1
10

题目思路

一道非常经典的模拟题，相当有阅读量与理解量。但是只要根据题目约束安排任务即可：

题目中有三个重要的约束：

  • 按照输入顺序依次安排任务
  • 第i+1道工序的开始时间必须在第i道工序之后
  • 如果某一间隔可以塞下这一工序，则直接放入，越早越好

在数据上，我们需要得到在何时插入这个工序，定义为 insert_time

那么大体上来说，代码结构为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main()
{
    q = []; // 工序数组
    for ...{ 
        cin ...
    } 
    // 若干预处理
    for(int i=1;i<=q.size();i++){
        insert_time = 第(i-1)道工序结束的时间;
        while(true){
            ...
            // 遍历每一个区间并寻找到合适区间
        }
        ...
        // 数据的更新
    }
}

变量设计

根据题目的三个约束，这里定义两个数组：

  1. 每个零件的最新进度：work_time[]
    此数组的检索为零件序号，内容为这一零件的最新工序的结束时间。对于零件i，即有：

  2. 对于每个机器，定义其时间轴数组为: time_line[a][b]
    此数组的检索a为机器型号，检索b为时间点，如果在机器a在第b秒需要为零件c工作，则记为：

    1
    time_line[a][b] = c;

对于输入的工序流程，需要知道的数据包括：这一步是为了哪个零件、这一步需要哪个机器以及这一步的用时是多少，所以对于每一个步骤这里都将整合在一个结构体中：

1
2
3
4
struct step{
	int t, id_m, id_i;	
};
map<int, step> q;

关键步骤：找区间

附上本人代码边看边解释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int s = insert_time;
// 定义区间初始位置
int have_work_point = 0;
// 定义工作位置标识 
while(true){
	bool isOk = true;
    for(int j=s;j<(s+q[i].t);j++){
        // 从空闲开头遍历这一工序需要的每一个时间
   	    if(time_line[q[i].id_m][j]!=0){
            // 时间轴上出现被占用的情况，不符合
   		    have_work_point = j;
            // 标记在工作的时间，方便找到下一个空闲区间
   		    isOk = false;
   		    break;
   	    }
    }
    if(isOk){
   	    insert_time = s;
        // 找到目标，就在空闲区间开始的位置插入新工序
   	    break;
    }else{
   	    while(time_line[q[i].id_m][have_work_point]!=0)
   		    have_work_point ++;
   	    s = have_work_point;
        // 寻找下一个区间
    }
}

最终代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
int m,n,res=0;
struct step{
	int t, id_m, id_i;	
};
map<int, step> q;
int time_line[25][10010];
int work_time[25];
int main()
{
	cin >> m >> n;
	for(int i=1;i<=(m*n);i++){
		cin >> q[i].id_i;
	}
	for(int i=1;i<=n;i++){
		int machine_id[25] = {0};
		for(int j=1;j<=m;j++){
			cin >> machine_id[j];
		}
		int flag = 1;
		for(int j=1;j<=(m*n);j++){
			if(q[j].id_i == i){
				q[j].id_m = machine_id[flag];
				flag ++;
			}
		}
	}
	for(int i=1;i<=n;i++){
		int time_set[25] = {0};
		for(int j=1;j<=m;j++){
			cin >> time_set[j];
		}
		int flag = 1;
		for(int j=1;j<=(m*n);j++){
			if(q[j].id_i == i){
				q[j].t = time_set[flag];
				flag ++;
			}
		}
	}
    //初始化，制作每一个步骤的结构体
	for(int i=1;i<=q.size();i++){ 
		int insert_time = work_time[q[i].id_i];
		int s = insert_time;
		int have_work_point = 0;
		while(true){
			bool isOk = true;
			for(int j=s;j<(s+q[i].t);j++){
				if(time_line[q[i].id_m][j]!=0){
					have_work_point = j;
					isOk = false;
					break;
				}
			}
			if(isOk){
				insert_time = s;
				break;
			}else{
				while(time_line[q[i].id_m][have_work_point]!=0){
					have_work_point ++;
				}
				s = have_work_point;
			}
		}
		for(int j=insert_time;j<insert_time + q[i].t;j++){
			time_line[q[i].id_m][j] = q[i].id_i;
		}
		work_time[q[i].id_i] = insert_time + q[i].t; 
	} 
	for(int i=1;i<=n;i++){
		if(work_time[i] > res) res = work_time[i];
	}
	cout << res << endl;
	return 0;	
}