基于BS模型条件下的期权价格改变策略

BS模型基本假设

研究的背景为风险中性、无套利的欧市市场，因此我们有：

$$C(X, S_t, r_{t,\tau}, \tau) = e^{-r_{t,\tau}, \tau} \int_0^{\infty} \psi(S_T, X)f(S_T)dS_T$$

其中，$\tau = T - t$ 为当前时间和交易日的差值，$X$为执行价(Strike Price)，$r$为无风险利率(risk-free rate),$f(S_T)$为资产价格分布，$\psi(S_T, X) = \max\left\{S_T - X\right\}$。

在Black-Scholes模型的定义中，标的资产价格$S_t$(State Price)为Geometric Brownian运动，则${S_t}$符合正态指数分布。

同时，期权价格$C$(Option Price)与$S_T$有：

$$f(S_T) = e^{r_{t, \tau}, \tau} \frac{\partial^2C}{\partial X^2}|_{X=S_t}$$

其中

BS模型改进方案

我们通过改变传统的指数正态分布使得BS模型拟合的更加精准。具体的，我们定义$S_t$符合混合分布，即：

$$h(\ln(S_T)) = \int\phi(\ln{S_T}|\mu, \sigma^2) dG(\mu, \sigma)$$

其中，正态分布满足 $\ln(S_T) \sim \mathcal{N}(ln(S_t) + (r_{t, \tau} - \delta -\sigma^2)\tau, \sigma\sqrt\tau) $ ,进一步有：

$$f(S_T) = \int v(S_T|\mu, \sigma^2) dG(\mu, \sigma)$$

其中$v$为符合上述正态分布的指数正态分布函数。那么对应的期权价格也有混合分布的形式：

$$\begin{align*} C(X, G) &= e^{-r_{t, \tau}\tau} \int\psi(S_T)f(S_T)dS_T \\ &= \int\int e^{-r_{t, \tau}\tau}\psi(S_T)v(S_T|\mu, \sigma^2)dS_TdG(\mu, \sigma)\\ &\equiv\int C(X, \mu, \sigma^2) dG(\mu, \sigma) \end{align*}$$ $$\begin{align*} C(X, \mu, \sigma^2) &= e^{-r_{t, \tau}\tau}\int\psi(S_T)v(S_T|\mu, \sigma^2)dS_T \\ &= e^{-r_{t, \tau}\tau}\int_{-\infty}^{\infty}(e^{S_T} - X) + \phi(s|\mu, \sigma^2)ds \\ &= e^{-r_{t, \tau}\tau + \sigma^2/2 + \mu}\overline{\Phi}\left(\frac{\ln(X) - (\mu + \sigma^2)}{\sigma}\right) - e^{-r_{t, \tau}\tau}\overline{\Phi}\left(\frac{\ln(X) - \mu}{\sigma}\right) \end{align*}$$

其中 $\overline{\Phi}(\cdot) = 1 - \Phi(\cdot)$

具体计算策略

优化问题陈述

我们通过收集：

• $\mathbf{C}$: 实际期权价格
• $\mathbf{x}$: 实际执行价
• $r, \delta, T$: 用于计算的参数

构造最小二乘优化问题：

$$\begin{align*} \hat{G} &= \argmin_{g\in G} \sum_{i=1}^{n} (C(x_i, G) - \mathbf{C}_i)^2 \\ &=\argmin_{\left\{\mathbf{\pi}, \mathbf{\mu}, \sigma\right\}} \sum_{i=1}^{n} \left(\sum_{j=1}^{n+1} \pi_j C(x_i, \mu_j, \sigma^2) - \mathbf{C}_i\right)^2 \end{align*}$$

其中，$\pi_j$为混合分布的权重，满足$\sum_{j=1}^{n+1}\pi_j = 1$。

约束条件分析

根据无风险套利市场规则，我们有未来资产价格的期望值为当前资产价格的贴现值：

$$E[S_T] = S_t e^{(r - \delta)\tau}$$

进一步有：

$$\begin{align*} \int e^{\mu + \sigma^2/2}dG(\mu, \sigma) &= S_t e^{(r - \delta)\tau} \\ S_t e^{\sigma^2/2} \sum_{j=1}^{n+1}\pi_j e^{\mu_j} &= S_t e^{(r - \delta)\tau} \\ e^{\sigma^2/2} \sum_{j=1}^{n+1}\pi_j e^{\mu_j} &= e^{(r - \delta)\tau} \\ \end{align*}$$

优化问题求解

1. 猜测$\sigma^2$, 并且对$\mu_j$进行初始化

2. 假设$\sigma^2$, $\mu_j$已知，求解$\pi_j$: 使用二次规划算法求解

3. 使用牛顿-莱布尼茨法求 $\mu_j$

AMD公司的期权价格分析

期权价格数据拟合

我们通过上述方法对AMD公司的期权价格进行分析，我们提取了2018年AMD公司6月7月的期权价格数据。我们将其分割为两个部分，对应$\tau = 0.0958$和$\tau = 0.08493$。

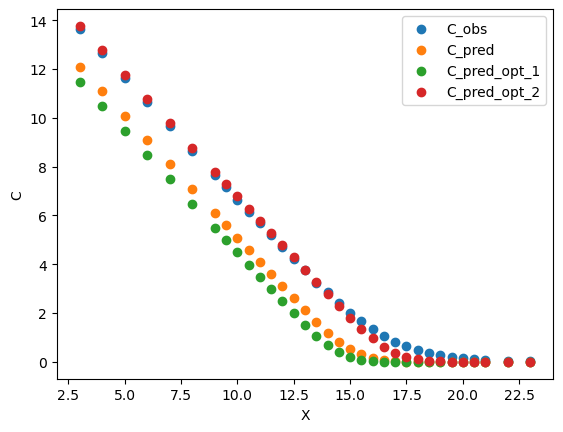
此图为训练集的期权价格分布，我们可以看到，期权价格分布在不同的执行价上有不同的分布。

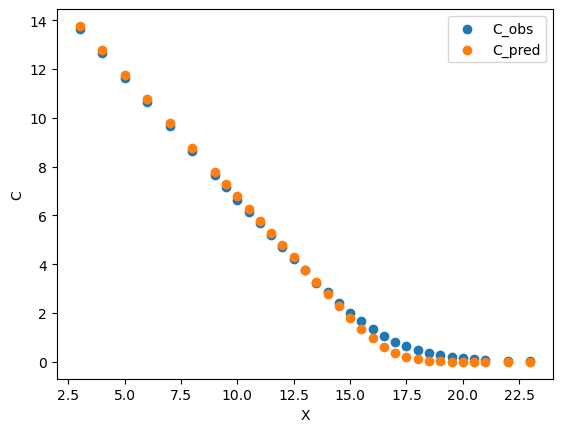
此图为测试集的期权价格分布，我们可以看到拟合较好。

Greeks分析

我们通过对期权价格的混合分布进行分析，得到了期权价格的Greeks值:

• Delta: $\Delta = \frac{\partial C}{\partial S}$ 代表期权价格对标的资产价格的敏感程度

• Theta: $\Theta = \frac{\partial C}{\partial \tau}$ 代表期权价格对时间的敏感程度

• Gamma: $\Gamma = \frac{\partial^2 C}{\partial S^2}$ 代表Delta对标的资产价格的敏感程度

• Vega: $\nu = \frac{\partial C}{\partial \sigma}$ 代表期权价格对波动率的敏感程度

• Rho: $\rho = \frac{\partial C}{\partial r}$ 代表期权价格对无风险利率的敏感程度

参考文献

1. Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of political economy, 81(3), 637-654.

2. MING, Y(2009). STATE PRICE DENSITY ESTIMATION VIA NONPARAMETRIC MIXTURES. The Annals of Applied Statistics, 3(3), 963–984